Calcul diffusion Compton et Zitterbewegung

De Transactional Quantic
Aller à : navigation, rechercher

Résumé

En 1927, Erwin Schrödinger avait présumé prouver que la diffusion d'un photon gamma ou X par un électron étudiée par A. Compton, relevait de la loi de Bragg, par interférences sur les réseau d'ondes brogliennes. Toutefois cette démonstration était prématurée et est erronée : seul le réseau d'ondes temporairement stationnaires dans le repère du centre d'inertie, résultant du battement entre les ondes Dirac-Schrödinger (= Zitterbewegung) de l'aller et du retour de l'électron, donne la bonne équidistance requise par la loi de Bragg. L'équidistance Bragg-Schrödinger est électromagnétique.

Les conditions de Bragg impliquent une largeur et une profondeur d'au moins une douzaine de distances interatomiques pour la largeur et la profondeur de l'interaction entre électron et photon. C'est incompatible avec le mythe des "aspects corpusculaires", mythe pourtant hégémonique à ce jour.

Abstract

In 1927, Erwin Schrödinger presumed to have shown that the Compton scattering between an electron and a X photon, is relevant of the Bragg law, computed in the frame of the center of inertia. However, his demonstration could not use in 1927 the right equidistance for the Bragg law. Only the Dirac-Schrödinger electromagnetic waves, whose spatial and temporal frequencies are the double of the Broglian (spinorial) ones, provide the right equidistance for the Bragg law. The lattice of electromagnetic planes that reflect the photon, results of the superposition of incoming and departing electronic waves.

The Bragg conditions imply at least a dozen of interatomic distances for both the depth and the width of the interacting photon and electron. So once again, there are no "corpuscular aspects" in the real physical world. Only waves, emitters and absorbers.

Rappel du calcul relativiste dans le repère du laboratoire

Calcul relativiste d'après "Mécanique quantique" de Greiner p 3 : Wolfgang Greiner, Quantum Mechanics, an Introduction :

Conservation de l'énergie:

LaTeX: h\nu= h\nu' + m_0c^2\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right)

Conservation de la quantité de mouvement selon l'axe du photon incident:

LaTeX: \frac{h\nu}{c}=\frac{h\nu'}{c}cos\theta + m_0c\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right)cos\phi

et selon l'axe perpendiculaire où la quantité de mouvement est nulle

LaTeX: 0=\frac{h\nu'}{c}sin\theta- m_0c\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right)sin\phi

En résolvant ces équations, on obtient

LaTeX: \lambda -\lambda'=\frac{h}{m_0\c}\ sin^2\ \frac{\theta}{2}

... Fin de l'emprunt.

On la refait, mais cette fois dans le repère du centre d'inertie, même s'il est expérimentalement irréalisable d'expérimenter dans ce repère, dont l'occurrence est aléatoire : on ne choisit pas à l'avance l'angle de diffusion, on reste prisonniers du repère du laboratoire.

Dans le repère du centre d'inertie

Compton epure.png

Là les calculs se simplifient puisque le photon ne change ni de fréquence ni d'énergie, juste de direction. Fixons qu'il arrive de la gauche, en descendant d'un angle LaTeX: \alpha = \frac{\theta}{2}, et continue en remontant du même angle. L'électron ne change pas d'énergie, mais juste de sens de la vitesse. On néglige l'énergie de liaison initiale de l'électron au solide.

Impulsion selon z'z transmise par le photon à l'électron : - LaTeX: \frac{h\nu}{c}.2\sin\alpha (signe - : descendante si l'axe z'z est vertical montant).

Equilibrée par le changement de celle de l'électron : LaTeX: 2m_ev (premier calcul non relativiste)

LaTeX: 2m_e c\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right) forme relativiste.

D'où la vitesse d'arrivée et de fuite de l'électron : LaTeX: v \hspace{4}=\hspace{4} \frac{h\nu}{m_ec}.\sin\alpha (premier calcul non relativiste)

On en déduit sa vitesse de phase : LaTeX: V \hspace{4}=\hspace{4} \frac{c^2} v \hspace{4}=\hspace{4} \frac{m_ec^3}{h\nu.\sin\alpha}

Or on connaît bien la période intrinsèque de l'électron, LaTeX: T_e \hspace{4}=\hspace{4} \frac{h}{m_ec^2}

D'où sa longueur d'onde broglienne : LaTeX: \lambda_e \hspace{4}=\hspace{4} V.T_e \hspace{4} = \hspace{4} \frac{V}{\nu_e} \hspace{4} = \hspace{4} \frac{m_ec^3}{h\nu.\sin\alpha}.{\frac{h}{m_ec^2} \hspace{4}=\hspace{4} \frac{c}{\nu.\sin\alpha}

On remarque que cette longueur d'onde ne dépend pas du tout de la masse de l'électron, et serait la même pour toute autre particule (chargée ou même pas chargée) sujette à diffusion Compton. Elle ne dépend pas non plus de la constante de Planck. Elle ne dépend que l'angle de déviation du photon, et de sa période ou de sa longueur d'onde avant et après la diffusion.

Guidés par ce que nous savons déjà faire en réfraction et réflexion sur un dioptre, il nous faut calculer l'émission du miroir à photon, qu'a constitué cet électron.
La partie horizontale, selon l'axe x'x, est invariante. Sa longueur d'onde est LaTeX: \frac{\lambda}{\cos\alpha}
La longueur d'onde de la partie pénétrante, et aussi bien de la partie réfléchie du photon est LaTeX: \frac{\lambda}{\sin\alpha} \hspace{4}=\hspace{4} \frac{c}{\nu.\sin\alph

Ces deux longueurs d'onde, celle de l'électron rebondissant, et de la partie réfléchie du photon, sont égales.


Il ne reste plus qu'à choisir entre les deux énoncés :
"La diffusion Compton prouve le caractère corpusculaire du photon", ou
"La diffusion Compton prouve le caractère ondulatoire de l'électron".

Or il n'y a pas à tortiller, cette émission de photon partiel montant, et absorption de photon partiel descendant, est bien due à l'accélération de l'électron selon z.

Jusqu'ici, le calcul n'a pas pu donner l'ordre de grandeur des extensions spatiales du photon X et de l'électron. On sait juste, pour avoir assez utilisé la raie LaTeX: K\alpha du molybdène en radiocristallographie des métaux, que sa longueur d'onde est comparable avec les distances interatomiques dans les métaux, et que les électrons de la liaison métallique sont peu liés, et surtout peu localisés, s'étendant sur une à plusieurs dizaines de distances interatomiques. Cela joint aux exigences géométriques de la diffraction sur des plans interatomiques, amène à conclure que et le photon, et l'électron sont larges et profonds de quelques dizaines de distances interatomiques tout au long de leur interaction Compton.

Application numérique pour la raie 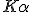LaTeX: K\alpha moyenne du molybdène :

Prenons un cas de forte déviation du photon, deux fois 30°, soit LaTeX: \sin\alpha = \frac 1 2

La longueur d'onde moyenne de la raie incidente est 0,070926 nm

D'où la projection anti-intérieure sur la direction de propagation de l'électron : LaTeX: \lambda _{Broglie} = 0,070926 nm x 2 = 0,141852 nm.

D'où l'on tire la vitesse de l'électron : LaTeX: v = \frac{\lambda _{Compton}}{\lambda _{Broglie}}.c = \frac {2,42631}{141,852}. 299792458 m/s = 5,1278 . 10 ^6 m/s

Soit une vitesse non relativiste, 1,7% de c. Et ce serait encore moins relativiste aux basses déviations.

Puis passer dans le repère de l'électron entrant...

Puis passer dans le repère de l'électron entrant, qui sera assimilé à celui du labo, et l'on devrait retrouver les formules expérimentales d'Arthur Compton.


Avec toutefois les sources d'erreurs suivantes :

  1. Un électron de valence n'est pas au repos, mais au niveau de Fermi, et à la vitesse de Fermi dans le métal.
  2. Et le procédé de calcul a négligé son énergie de liaison, métallique.

C'est le n° 1, le niveau de Fermi, la source la plus grosse d'élargissement des raies Compton, en plus du fait que la raie X LaTeX: K\alpha est un doublet.

Et l'objection de principe qu'on a juste constaté l'échange des vecteurs d'onde, sans faire la physique de l'interaction

Composante verticale du vecteur d'onde gamma entrant = vecteur d'onde électronique sortante.

Composante verticale du vecteur d'onde gamma sortant = vecteur d'onde électronique entrante.

Mais à ce stade du calcul, la physique de l'interaction nous est encore inconnue.

L'échec est garanti si l'on tente d'étendre à ce domaine la modélisation en objet massif qui ralentit, puis repart dans l'autre sens, avec une accélération moyenne finie durant le temps de l'interaction. En 1926 (Schrödinger 1926) Erwin Schrödinger nous avait montré le chemin en montrant que l'émission d'un photon est le résultat du battement d'une onde électronique entre son état final et son état initial. Ici aussi, il faut faire battre entre eux l'état initial "montant" et l'état final "descendant" (selon le sens choisi pour la figure). Durant ce battement, un état intermédiaire contient une onde broglienne stationnaire.

Il apparaît une autre contrainte, dont nous ne savons pas si elle a été expérimentalement vérifiée : la polarisation électrique est nécessairement dans le plan de la figure.

Condition de Bragg et Zitterbewegung

Rappelons la condition de Bragg en radiocristallographie :

Si d est la distance interréticulaire, LaTeX: \alpha = \frac{\theta}{2} est l'angle du rayon incident sur le plan réticulaire, ou moitié de l'angle de déviation totale, LaTeX: \lambda la longueur d'onde du rayonnement incident, et n un entier, ordre de la réflexion :

LaTeX: 2d. \sin\alpha = n\lambda

Condition Bragg.png

Preuve : arrivant sous l'angle α sur les plans réticulaires AB etc., l'onde monochromatique réfléchie par le plan suivant présente une différence de marche égale à BC - HC. La première réflexion n'existe que si BC - HC vaut exactement une longueur d'onde. Dans le triangle isocèle ABC, d = AB LaTeX: \sin\alpha = BC LaTeX: \sin\alpha
Tandis que dans le triangle rectangle BCH, CH = BC LaTeX: \cos2\alpha.
La différence de marche entre les deux ondes est BC - CH = BC LaTeX: (1 -\cos2\alpha) = 2 BC . LaTeX: (\sin^2\alpha) = 2 d LaTeX: \sin\alpha \hspace{4}=\hspace{4} n.\lambda_{\gamma}

Or la longueur d'onde broglienne calculée ci-dessus ne nous donne que la réflexion d'ordre deux : LaTeX: \lambda_e \hspace{4}=\hspace{4} \frac{\lambda_{\gamma}}{\sin\alpha} .
Une réflexion de faible intensité, tandis que devrait apparaître à l'expérience l'autre réflexion, d'ordre 1, forte, qui n'est jamais observée (et qui violerait les lois de conservation de l'impulsion-énergie)...


Bon sang ! Mais c'est bien sûr ! C'est l'onde électromagnétique stationnaire à fréquence temporelle et à fréquence spatiale doublée, le Zitterbewegung, ou Tremblement de Schrödinger conforme à l'équation de Dirac, qui donne la bonne équidistance réticulaire de Bragg, exactement d !

LaTeX: d \hspace{4}= \hspace{4} \frac {\lambda_e}2 \hspace{4}= \hspace{4} \frac{T_e}{2 v_e} \hspace{4}= \hspace{4} \frac{h}{2 m_e.v_e} \hspace{4} = \hspace{4} \frac{\lambda_{\gamma}}{2\sin\alpha}

Diffusion Compton.png

Quod Erat Demonstrandum !

C'est bien la fréquence spatiale du Tremblement de Schrödinger, stationnaire durant la réflexion de l'électron sur le photon, qui satisfait à la condition de Bragg pour un réflexe au premier ordre, donnant exactement la diffusion Compton du photon incident.

On se proposait de mettre en évidence le mécanisme physique et ondulatoire qui rendrait compte de la diffusion Compton. Mission accomplie : c'est l'équidistance des ondes temporairement stationnaires de Dirac-Schrödinger qui satisfait à la condition de Bragg, pour la diffusion au premier ordre.

Bibliographie et références

E. Schrödinger. Über den Comptoneffect. Annalen der Physik. IV. Folge, 62. http://www.apocalyptism.ru/Compton-Schrodinger.htm

J. Strnad. The Compton effect — Schödinger's treatment. Eur. J. Phys. 7 (1986). http://www.apocalyptism.ru/Compton-effect.htm

Adresses signalés par : Lev Lvovitch Regelson. Compton effect: Schrödinger's treatment in : The Science Forum - Scientific Discussion and Debate. http://www.thescienceforum.com/viewtopic.php?p=235655 Lien changé : http://www.thescienceforum.com/physics/18025-compton-effect-schroedingers-treatment.html

P.A.M. Dirac. The Principles of Quantum Mechanics. Oxford University Press, ed 1958.

W. Greiner. Relativistic Quantum Mechanics ; Wave Equations. Springer 1997.


Liens sur le Zitterbewegung :

http://en.wikipedia.org/wiki/Zitterbewegung

http://www.springerlink.com/content/g75q8g1j4h20w5p6/

http://arxiv.org/PS_cache/arxiv/pdf/0909/0909.2004v3.pdf

http://wigner.elte.hu/science/?q=node/66

http://prb.aps.org/abstract/PRB/v74/i17/e172305

http://ajp.aapt.org/resource/1/ajpias/v20/i8/p479_s1

The detailed motion of a free Dirac electron is investigated by examining the expectation values of the position r and of r×math in a wave packet. It is shown that the well-known zitterbewegung may be looked upon as a circular motion about the direction of the electron spin, with a radius equal to the Compton wavelength (divided by 2π) of the electron. It is further shown that the intrinsic spin of the electron may be looked upon as the “orbital angular momentum” of this motion. The current produced by the zitterbewegung is seen to give rise to the intrinsic magnetic moment of the electron.

Kerson Huang

Department of Physics and Laboratory for Nuclear Science and Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts

http://adsabs.harvard.edu/abs/1952AmJPh..20..479H : même article.

http://www.valdostamuseum.com/hamsmith/Sidharth.html

http://geocalc.clas.asu.edu/pdf-preAdobe8/ZBW_I_QM.pdf consultable à l'écran en aperçu :

http://www.google.fr/url?sa=t&source=web&cd=30&ved=0CHYQFjAJOBQ&url=http%3A%2F%2Fgeocalc.clas.asu.edu%2Fpdf-preAdobe8%2FZBW_I_QM.pdf&rct=j&q=Zitterbewegung%20Compton&ei=hj3YTbH7BdSwhQew7Ky4Bg&usg=AFQjCNGibaLphwFiWngyIsBjNXXj-8JBZA&cad=rja

http://www.ps.uci.edu/~markm/eee/P113C_reference_material/gingrich_relativistic_quantum_mechanics/Klein%20Gordon/Zitterbewegung.pdf

Récupérée de « http://deontologic.org/quantic/index.php?title=Calcul_diffusion_Compton_et_Zitterbewegung&oldid=8 »