Revision as of 23:51, 19 November 2014

Prérequis : Les grandeurs physiques

Un vecteur, comme son nom l'indique, c'est pour les translations

Un vecteur, comme son nom l'indique, c'est pour les translations, et et c'est pour tout ce qui se déduit directement des translations, en physique : vitesse, accélération, quantité de mouvement, force, champ électrique, dipôle électrostatique, vitesse de diffusion ionique. Aller d'un départ vers une destination.

Comme son nom l'indique ?

La racine vagh, en indo-européen, désignait le chariot. Elle a donné des centaines de descendants, dont plusieurs dizaines en français.

Rappel de vocabulaire : Le mot "vector" était déjà pris depuis plus de 42 siècles, avant d'être réutilisé en 1837 par W. R. Hamilton (1805 - 1865), à l'usage des mathématiciens et des physiciens. Dans le dictionnaire de latin, on trouve une famille de plus de 100 termes autour du verbe "vehere", des noms "vector" (au sens de chariot, puis d'animal bâté ou de trait, de cavalier ou de passager d'un navire), et "veha" (voie). En français, nous avons gardé : véhicule, voie, voyer, dévier, convecteur, vexer, convexe, vétérinaire. La famille est également riche dans les langues germaniques : Weg, thalweg, Norvège, Solveig, tramway, wagon, vaguemestre... On la retrouve aussi dans les langues slaves.

Depuis des millénaires, nous rencontrons l'usage littéral : est vecteur ce qui véhicule quelque chose. Une flèche incendiaire tirée depuis un arc à corde très lâche, fut un vecteur de combustion, capable de provoquer un incendie dans les fortifications en bois de l'adversaire. Au 18e siècle, les colporteurs furent les vecteurs des pamphlets révolutionnaires. Certaines fusées sont des vecteurs nucléaires. Le moustique est le vecteur de la fièvre jaune et du paludisme.

En second et depuis 1837, nous rencontrons sa mathématisation immédiate (mais correcte), pour les besoins de la physique macroscopique : est vecteur ce qui caractérise une translation. Ce cahier des charges est rempli par la définition de Bellavitis : les vecteurs comme classes d'équivalences des bipoints par la relation d'équipollence. La sémantique précédente est donc conservée, dans ses grandes lignes, mais connaît une schématisation. Du point de vue mathématique, et dans le langage axiomatique que nous devons aux écoles de Klein et de Hilbert, nous avons besoin des axiomes des espaces vectoriels, plus une métrique, plus le moyen de définir une translation. Ce qui implique que l'espace en question soit au moins approximable localement par un espace affine pseudo-euclidien tangent. Du point de vue pratique, cela signifie que l'on peut valablement dessiner, et se servir de ses mains, d'une règle, d'un compas, d'une équerre, ou de ses pas, ou de ses outils d'atelier, pour se guider dans les raisonnements.

Par extension légitime, est aussi considéré comme vecteur, tout ce qui dérive du vecteur de translation, par une dérivation ou intégration selon une variable qui n'est pas d'espace (le temps, notamment), ou par multiplication par une grandeur, dont la dimension physique ne comprend aucune longueur, à quelque puissance que ce soit.

Définition : de la translation, à la classe d'équipollence des bipoints

Le cahier des charges est de caractériser l'opérateur de translation. La définition formelle répondant à ces réquisitions, définit le vecteur comme classe d'équivalence de bipoints, par la relation d'équipollence. Cette définition n'est pas la définition minimaliste des espaces vectoriels abstraits. Mais c'est la plus petite qui couvre toutes les propriétés géométriques réellement utilisées par la physique élémentaire macroscopique.

Nos nombres entiers, si familiers, sont aussi des classes d'équivalence : 2 n'est pas une paire de vaches, ni une paire de cailloux, mais est ce qu'il y a de commun à une paire de vaches, une paire de cailloux, une paire de claques, etc. par la relation : {il existe une bijection entre ces deux collections}.

Dans un espace E, comme notre espace ordinaire de la géométrie, les bipoints servent à résumer un déplacement, avec un point de départ, et un point d'arrivée.

Un bipoint : c'est un couple de points, respectivement le premier, ou point de départ, et le second, ou point d'arrivée. On le note (A,B). Les extrémités d'intervalles finis sur une droite, forment de tels bipoints.

Mettre deux bipoints bout à bout

On peut définir une addition : si le départ du second, est exactement l'arrivée du premier,

(A,C) = (A,B) + (B,C).

Exemple : se rendre de Paris à Lyon, puis de Lyon à Marseille, revient à se rendre de Paris à Marseille. Puisqu'on ne s'intéresse qu'au point de départ, et au point d'arrivée.

C'est la relation de Chasles.

On ne sait pas multiplier un bipoint par une constante. Mathématiquement, autant dire qu'on ne sait presque rien faire avec des bipoints.

Si le parallélisme existe, on peut définir l'équipollence de deux bipoints

Ajoutons l'hypothèse que dans notre espace E, le postulat d'Euclide soit vérifié : la parallèle d'une droite passant par un point, existe, et est unique. Dans ce cas, les parallélogrammes existent.

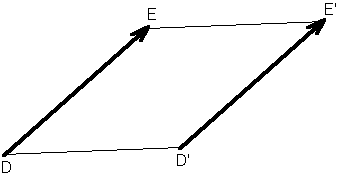
Définition : Les bipoints (D,E) et (D',E') sont dits équipollents si le quadrilatère DEE'D' est un parallélogramme.
C'est une relation réflexive, réciproque et transitive : une relation d'équivalence.

Définition : un vecteur est la classe d'équivalence de bipoints, par la relation d'équipollence. Un vecteur peut prendre une infinité de bipoints comme représentants de la classe.

De l'addition des bipoints, on déduit l'addition des vecteurs : pour tous points A, B, et C, = + .
Sauf que cette fois, c'est la classe d'équipollence représentée par le bipoint (A,C), qui est bien la somme de la classe d'équipollence représentée par le bipoint (A,B) et de la classe d'équipollence représentée par le bipoint (B,C), et on est libres de choisir d'autres représentants, les représentants qui nous sont les plus commodes.

Dans un espace euclidien, et grâce aux parallélogrammes, on peut transporter les extrémités d'un bipoint, les éléments caractérisant une translation. Plus tard, pour parler d'orthogonalité, nous aurons besoin de choisir une norme euclidienne parmi toutes celles possibles. En effet, les expériences de mesures courantes dans notre espace humain sont compatibles avec le postulat d'Euclide, et avec le postulat qu'il existe bien une orthogonalité. Tant que les vitesses des objets dans le laboratoire sont faibles devant celle de la lumière, la longueur d'un objet ne dépend pas de son orientation dans l'espace, sous réserve qu'il soit mécaniquement indéformable. Sous réserve aussi que les trajets de la lumière dans le vide soient représentatifs de l'idée que nous nous faisons de la ligne droite, ce qui est bien réalisé à la surface de la Terre, astre modeste, à la gravité modeste.

De cette définition, il résulte qu'on peut additionner entre eux les vecteurs de même nature, les multiplier par un nombre, et par une grandeur physique non géométrique. Et par une grandeur géométrique, telle qu'un autre vecteur ? Là c'est un chapitre ultérieur de la géométrie, ou analyse tensorielle, dans laquelle ces vecteurs que nous venons de définir, sont inclus comme tenseurs d'ordre 1.

Quatre projections pour la physique

Projections quelconques

Puisque nous savons faire la somme et la différence de deux vecteurs, nous savons projeter sur un sous-espace, parallèlement à un sous-espace complémentaire.
Ces projections sont indispensables en cristallographie : projeter parallèlement aux autres axes cristallographiques du cristal, qui ont rarement la gentillesse d'être orthogonaux entre eux.

Projections orthogonales, intérieure et extérieure

Le choix le plus simple, physiquement le plus fécond, est de prendre la direction perpendiculaire.

Prenons désormais le choix de projection orthogonale à D. La décomposition de est alors unique :

= + .

On désigne le restant de l'opéra­tion projec­tion, , la projection extérieure de sur D.

est la projection intérieure.

D'où il viendra la définition sommaire du produit intérieur : produit d'un vecteur, par la projection intérieure de l'autre.

Et la définition sommaire du produit extérieur : produit d'un vecteur, par la projection extérieure de l'autre.

Ceci est indispensable à la physique. On l'étend facilement aux tenseurs d'ordre supérieur.

Avec un plan P et un vecteur, on définit de la même façon, la projection intérieure sur ce plan : , et la projection extérieure au plan : , qui est orthogonale à tout vecteur de P.

En considérant les covecteurs inverses (sur un espace métrique), on définit de même les projections anti-intérieure, et anti-extérieure.

Coordonnées d'un vecteur.

Repère

On ne peut décrire une position d'un point que par rapport à un repère.

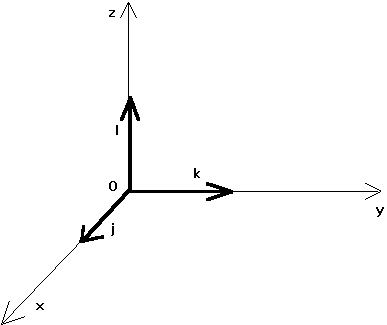
Un repère cartésien (le plus utilisé) se compose d'une origine, d'exactement autant de directions d'axes qu'il en faut (par exemple 2 en géométrie plane, 3 en géométrie dans l'espace), et du même nombre de vecteurs unitaires sur chaque axe.

Unitaire, signifiant qu'il est de longueur unité.

On se simplifie beaucoup la vie, quand on peut choisir des axes orthogonaux entre eux, et ayant la même unité de longueur sur chaque axe. On appelle un tel repère, un repère orthonormé.

Dans la géométrie courante, on peut faire ce choix d'orthonormalité, et on le fait systématiquement. Si notre métier s'occupait de cristaux (cristaux métalliques, comme dans tous les métaux et alliages, ou cristaux minéraux, comme dans le mica, ou le quartz), parfois nous pourrions prendre un repère orthonormé dans le cristal (cas du cuivre, de l'aluminium), et d'autres fois, ce choix serait désastreux (cas du mica, du quartz, du magnésium, du zinc, du titane, etc...). Les cristallographes (ceux dont le métier s'occupe de cristaux, par exemple pour étudier des piézoélectriques, des ferromagnétiques, des supraconducteurs) préfèrent de loin prendre un repère qui épouse les directions et unités du cristal. Il leur a donc fallu apprendre un peu plus de géométrie, et d'algèbre linéaire, pour rester capables de calculer juste, à partir de repères non orthogonaux, et dont les unités selon les axes ne sont pas nécessairement égales. Même problème en mécanique des élastomères : un repère lié à la matière au repos, n'est plus orthonormé, ni même euclidien, quand la matière est déformée.

Avoir choisi un repère, permet de privilégier une certaine sorte de projection : la projection sur les axes de coordonnées. Il est possible de projeter tout vecteur sur les axes du repère. Si on nomme , les axes de ce repère, on pourrait nommer , et les trois projections de sur ces trois axes. La règle du jeu à respecter, est que la projection se fasse parallèlement aux autres axes du repère. Si l'on est dans le plan, cela se réduit à : parallèlement à l'autre axe du repère. Tout vecteur se décompose ainsi de façon unique comme somme de deux (dans le plan) ou trois vecteurs, chacun parallèle à un axe de coordonnées.

Bases et coordonnées

La liste des vecteurs unitaires, énoncée dans un ordre fixe, est aussi appelée une base de l'espace E. Nous pouvons nommer distinctement les vecteurs de base, par exemple , , . Nous pouvons aussi leur donner un numéro, dit indice. Ils seront alors appelés e₁, e₂, e₃. Les débutants préfèrent la première façon de nommer les vecteurs de base. Les professionnels préfèrent (de beaucoup) la seconde façon.

Il est possible de projeter tout vecteur sur les axes du repère.

Si on nomme , les axes de ce repère, on peut nommer , et les trois projections ou composantes de sur ces trois axes : = + + .

On peut rapporter chaque projection (ou composante), au vecteur unitaire de cet axe. Soient V_x, V_y, V_z, les trois quotients :
= V_x.
= V_y.
= V_z.

Tout vecteur de l'espace E est décomposable sur la base, d'une seule façon, que voici :

= V_j + V_k + V_l = V₁ e₁ + V₂ e₂ +V₃ e₃ .

Les nombres V_j , V_k, V_l (ou V₁ , V₂ , V₃ , puisque par définition, ce sont les mêmes) sont nommés coordonnées de sur cette base. Chaque coordonnée est un quotient de deux vecteurs colinéaires : quotient d'une composante sur un axe par le vecteur unité de cet axe. Un vecteur se distingue d'une grandeur physique ordinaire, scalable, en ce qu'il faut plusieurs quotients à la fois, pour le décrire.

Par opposition, on nomme "scalaire" une grandeur physique qui se contente d'une seule coordonnée, et qui ne dépend pas des orientations ni des unités du repère géométrique.

Si pendant quelque temps, on ne change jamais de base (repère et vecteurs unitaires), on économise en écritures, en se contentant de désigner un vecteur par seulement ses coordonnées dans cette base.
On peut les écrire en ligne : (V₁ , V₂ , V₃), ou en colonne : , à condition que le début de validité de la base définie, ait été clairement précisé avant.

Ce qu'il ne faut plus faire

Oublier de mentionner la base, son unité et ses propriétés, est une omission trop courante. Cette négligence serait mortelle pour un calcul en cristallographie : tout serait faux. D'autant plus dangereuse qu'elle est tacite et inconsciente depuis les origine de l'usage des vecteurs au 19e siècle, cette négligence a vite produit de grosses incompréhensions, qui durent, qui durent... Ainsi depuis le 19e siècle, on s'est souvent imaginé qu'un vecteur ne serait rien de plus qu'une suite ou liste de nombres, en oubliant de l'accompagner de la règle de transformation de cette suite, à chaque changement de base, et d'une unité physique.

Ce qu'on peut faire et qui est une innovation

Rien ne nous interdit de généraliser les coordonnées, prendre de vraies grandeurs physiques - cohérentes, quand même - au lieu de simples nombres. Ainsi un repère géométrique pour les positions peut servir à définir les coordonnées d'une quantité de mouvement : ses vecteurs de base sont en mètres, les coordonnées de la quantité de mouvement sur cette base, seront en kilogrammes divisés par seconde. La quantité de mouvement est bien en kilogramme.mètre/seconde.

Addition de vecteurs par les coordonnées (sur la même base)

Aucune difficulté : on additionne les coordonnées homologues.

Soient les vecteurs et , de coordonnées et (coordonnées sur la même base !).

Le vecteur somme + a pour coordonnées : .
Même scénario pour la différence : différence des coordonnées.

Changement d'origine

Changement d'origine, pour les vecteurs de repérage des points de l'espace. L'origine était O. Désormais on prend O'. On applique la règle d'addition des bipoints :

Multiplication par un nombre, ou une constante "scalaire".

On multiplie toutes les coordonnées par la constante.

Symétries des vecteurs

Dimension 1 : Géométrie sur une droite

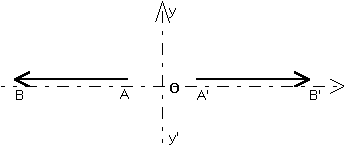
Symétrie par rapport à un point. Le vecteur est toujours retourné par cette symétrie.

Dimension 2 : Géométrie sur un plan

Il ne peut y avoir que deux sortes de sous-espaces invariants par la symétrie : un point ou une droite. Le point est un sous-espace de dimension nulle. La droite est un sous-espace de dimension un.

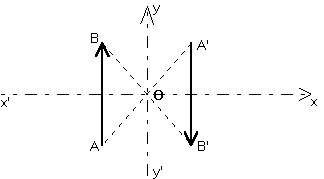
Symétrie par rapport à un point.

Le vecteur est toujours retourné par cette symétrie.

Alors que les grandeurs de second échelon, telles que les angles orientés, sont conservées !

Symétries par rapport à une droite.

Deux cas simples se présentent :
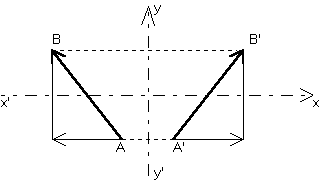
Le vecteur est parallèle à la droite invariante. Il est conservé.
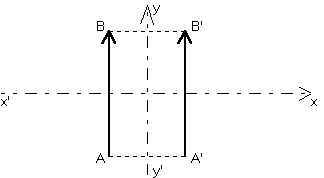
Le vecteur est perpendiculaire à la droite invariante. Il est retourné.

Cas général :

Vecteur ni perpendiculaire ni paral­lèle à la droite invariante. Alors la projection intérieure de V sur D est conservée, tandis que le restant, projection extérieure, est retourné.

Géométrie dans l'espace E₃ (affine à R³).

Il ne peut y avoir que trois sortes de sous-espace invariant par la symétrie : un point, une droite, ou un plan. Le plan est un sous-espace de dimension deux.

Symétrie par rapport à un point.

Le vecteur est toujours retourné par cette symétrie.

Symétrie par rapport à une droite.

Deux cas simples se présentent :

Le vecteur est parallèle à la droite invariante. Il est conservé.

Le vecteur est perpendiculaire à la droite invariante. Il est retourné.

Cas général : vecteur ni perpendiculaire ni parallèle à la droite invariante. Alors la projection intérieure de V sur D est conservée, tandis que le restant, projection extérieure, est retourné.

Symétrie par rapport à un plan.

Deux cas simples se présentent :

Le vecteur est parallèle au plan invariant. Il est conservé.

Le vecteur est perpendiculaire au plan invariant. Il est retourné.

Cas général : vecteur ni perpendiculaire ni parallèle au plan invariant. Alors la projection intérieure de V sur le plan P est conservée, tandis que le restant, projection extérieure, est retourné.

Les dessins se déduisent immédiatement des dessins valides en géométrie plane. Pas d'éléments vraiment nou­veaux. La symétrie par rapport à un plan se dessine en projection sur un plan, identiquement à la symétrie par rapport à une droite, si l'on choisit de projeter sur le plan qui contient les vecteurs symétriques.

Généralisation, en espace de dimension n.

La projection intérieure d'un vecteur sur un sous-espace invariant, est conservée.
La projection extérieure d'un vecteur sur un sous-espace invariant, est retournée.
Ça valait donc la peine de distinguer la projection extérieure de la projection intérieure.

A quoi les symétries sont-elles utiles ?

Les symétries servent à ramener de nouveaux problèmes à des problèmes connus et déjà résolus. Elles servent à se simplifier la vie, à prouver que des coordonnées sont nulles, ou égales, sans longs calculs. Elles servent à prouver que des effets sont nuls. En 1894, Pierre Curie (1859 - 1906) a énoncé le principe : L'effet est au moins aussi symétrique que la cause. Réciproquement, c'est la dissymétrie qui crée le phénomène.

Il existe de nombreuses autres sortes de symétries, que nous n'étudions pas ici.

Si on change de vecteurs de base ?

Supposons que je communique le résultat de mes travaux, à un ami et collègue ingénieur, qui travaille aux Etats-Unis. Moi, j'ai travaillé en mètres, l'unité légale en France de nos jours. Mais lui travaille en yards, en pieds et en pouces. Ou plus simplement, je voudrais communiquer mes travaux à un physicien âgé, qui a utilisé toute sa vie le centimètre comme unité légale, utilisée par les physiciens du monde entier, de son temps.

Je lui parle d'un vecteur long de 2 mètres. Pour me comprendre, il va traduire cela comme un vecteur long de 200 cm. Traduisons cela en coordonnées :

= (2,0,0) m = (200,0,0) cm.

On remarque que quand l'unité est 100 fois plus grande, alors les coordonnées sont 100 fois plus petites. Autrement dit, les coordonnées naturelles sont contravariantes : elles varient au contraire de la base. C'est indispensable, pour que ces coordonnées soient bien descriptrices du même vecteur physique.

Grandeurs vectorielles en physique

La somme vectorielle, sous la forme d'addition de vitesses, ou d'addition de forces, était maîtrisée dès le 17e siècle, par certains physiciens (pas tous...). Malgré ce que nos manuels nous font croire, ni Laplace (1749 - 1827), ni Ampère (1775 - 1836) n'ont connu le mot "vecteur", inventé en 1837, ni les notations vectorielles.

Unités de base de la physique

On peut rapporter toutes les unités de la physique, à un tout petit nombre d'unités de base, huit en tout :

1. L'unité de longueur (mètre), qui ne suffirait pas à la géométrie, sans...
2. le radian, quotient de deux longueurs perpendiculaires. Le radian est le grand oublié des physiciens. Sa généralisation comme quotient de deux grandeurs en quadrature de phase, n'a jamais été clarifiée. Nous reviendrons dans le chapitre suivant, consacré aux tourneurs, produits extérieurs de vecteurs.
3. L'unité de temps (seconde),
4. l'unité de masse (kilogramme),
5. l'unité de charge électrique (coulomb).

On peut symboliser ces cinq unités de base par les cinq majuscules : L, R, T, M, Q.

Les trois autres, le kelvin, la candela, la mole, ne nous serviront pas ici.

Chaque unité physique particulière, s'exprime comme un monôme généralisé des unités de base. Monôme généralisé, signifie : expression ne comportant que des multiplications et divisions. Les multiplications ou divisions multiples, peuvent se résumer par une élévation à une puissance. Cette puissance peut être négative, pour désigner une division. Par exemple, l'unité de vitesse, le mètre par seconde, a pour monôme : [L . T^-1].

Cet exposé est très classique. Nous verrons ultérieurement à quel point il est critiquable, et doit être révisé de fond en comble au regard de la mécanique symplectique, et du théorème de Noether.

Quelles sont les grandeurs physiques qui sont vectorielles ?

Quelles sont les grandeurs physiques qui sont vectorielles ?

Nature de la grandeur	Unité S.I.	Monôme dimensionnel
Déplacement	m	[L]
Vitesse	m/s	[L.T-1]
Accélération	m/s2	[L.T-2]
Impulsion (quantité de mouvement)	kg . m/s	[M.L.T-1]
Force	kg . m/s2	[M.L.T-2]
Champ électrique ()	volt/mètre = newton/coulomb	M.L.T-2 . Q-1]
Moment dipolaire électrostatique	C . m	[L.Q]
Elément de courant (C'est le I.dl figurant dans la loi de Laplace).	A . m = C . m /s	[L.T-1.Q]
Potentiel magnétique ()	unité d'impulsion/coulomb	[M.L.T-1 . Q-1]

Remarque : la grandeur "longueur" figure toujours une fois, à la puissance 1.

Les covecteurs sont les grandeurs de dimensions en [L^-1...], qui ont les mêmes propriétés de symétrie que les vecteurs (mais qui en diffèrent évidemment par leurs propriétés dimensionnelles). Plusieurs gradients considérés en chimie (lois de diffusion moléculaire ou ionique), ou en mécanique des fluides et en météorologie, sont des covecteurs, inverses de vecteurs. Vecteurs et covecteurs, composent le premier échelon dans la famille des tenseurs.

Enfin des capacités vectorielles volumiques, telles que le vecteur déplacement de Maxwell , peuvent être de dimension physique nette -2 relativement à l'unité de longueur : [L^-2...] : [L^-2 . Q] = [L . L^-3 . Q].

Suites  : Métrique des grandeurs vectorielles en physique
Les quart-de-tours entre vecteurs : tourneurs

Références et bibliographie

Syntaxe géométrique de la physique : projections et vrais vecteurs. http://jacques.lavau.perso.sfr.fr/SYNTAXV1_.htm