Difference between revisions of "Les grandeurs physiques"

Latest revision as of 23:49, 19 November 2014

Beaucoup plus de propriétés que les nombres, plus de contraintes et de garde-fous aussi

Abstraire ?

ABSTRAIRE : c’est se dispenser de regarder un certain nombre (souvent un très grand nombre) de propriétés et de particularités (étymologie : trahere tirer, ab hors de, à partir de). Autrement dit, en termes ensemblistes, une abstraction est un ensemble quotient par l’ensemble des classes d’équivalence. A charge pour l’analyste d’écrire noir sur blanc la relation d’équivalence, et d’exhiber les preuves que cela tient bien la route.

Corollaires : abstrait n’implique pas « mieux » ! C’est la tâche de l’analyste que de vérifier et de prouver que dans le procédé d’abstraction qu’il a choisi, il n’a pas commis de fautes professionnelles, qu’il n’a pas écarté des propriétés vitales. Ensuite il doit prouver que son abstraction est efficace en productivité, et enfin, si c’est possible, qu’elle est optimale.

L'abstraction maîtresse dans l'histoire de l'humanité, ce sont certainement les nombres.
Agés de trois semaines, nos bébés distinguent clairement un babar (poupée représentant l'éléphant Babar) de deux babars, deux babars de trois babars. Les pigeons et les pies adultes font aussi bien. C'est vers trois, quatre ou cinq objets identiques que ces capacités innées perdent pied, se laissent tromper. Une pie qui a vu quatre hommes (d'aspects similaires entre eux) entrer dans une cabane, et trois seulement en ressortir, ne flaire pas le piège : elle n'a pas repéré la différence si les habits et les apparences (par exemple les voix, ou les rythmes de gestes) sont suffisamment similaires.

Les nombres sont tout-abstraits. Le nombre "quatre" n'est pas "quatre ânes", ni "quatre cailloux", mais ce qui est commun entre eux, par la relation "On peut établir une bijection (une relation un pour un) entre ces deux collections", respectivement d'ânes et de cailloux. C'est donc une classe d'équivalence : la relation est symétrique, réflexive, transitive.
On sait que nos ancêtres Magdaléniens vivaient la lente et longue transition de chasseurs de rennes vers éleveurs de rennes. Ils savaient chasser des troupeaux vers des enclos, où ils pouvaient en choisir et en capturer, répartir cette propriété entre plusieurs familles de plusieurs clans. Ils ont donc dû inventer comment compter. Passer un caillou d'un tas à un autre à chaque animal qui entre dans un enclos, ou qui passe dans un sous-enclos, est une solution largement pratiquée. Une solution plus portative est de tailler une encoche dans un bâton, par animal de la collection. Les chiffres romains dérivent directement de cette numération primitive faite par des peuples de bergers.

Mais un nombre tout court, a des propriétés différentes d'un "nombre de quelque chose". Un troupeau de quatre oies n'a pas les propriété d'un troupeau de quatre rennes adultes, qui n'a pas les propriétés d'une harde de quatre mammouths... Un bosquet de quatre pins n'a pas les propriétés d'un bosquet de quatre bouleaux. Le nombre quatre est dispensé de tout cela. Les additions qui sont libres entre nombres, sont sérieusement contraintes entre nombres-de-quelque-chose.
D'une part les deux collections doivent être distinctes, sans éléments communs, et d'autre part leur réunion doit être encore un ensemble qui ait du sens et de l'usage, où les éléments aient quelque équivalence en commun.

Ensembles disjoints !

Sur le toit en terrasse d'une ancienne usine reconvertie en HLM, quelques appartements dépassaient, via un escalier en colimaçon, et un second étage construit en Siporex et une isolation externe. Ma fille fut vite séduite par un charmant chaton, qui venait nous rendre visite et laper tout ce qu'on lui donnait de bon à boire et à manger. Le chaton apprenait très sérieusement à chasser les pigeons. Toutefois d'un appartement-îlot voisin, un autre petit garçon appelait le chaton, pour la croustance et le rentrer la nuit. Si vous réunissez le chat de ma fille, et le chat du voisin, cela fait une collection de deux chats, ou d'un seul chat ?

Même genre : sur la fin de sa première traversée de l'Océan Atlantique, à bord du Kurun, Jacques-Yves Le Toumelin annonce à son équiper Fargue :
"Le premier qui aperçoit la terre aura droit à deux rasades de rhum, le second à un seul verre de rhum, et le dernier à un coup de pied au cul !"
"A quoi aura droit l'avant-dernier ?" réplique Fargue.
Voyons ? Le premier, le second, l'avant-dernier, le dernier, ça fait bien un équipage de quatre personnes ? Vous êtes sûrs ?
Après avoir débarqué son équipier à la Martinique, Le Toumelin continua seul son tour du monde.

Ça c'était pour la nécessité que les éléments des deux collections à réunir soient bien distincts, sans recouvrements.

L'ensemble réunion doit avoir une cohérence indiscutable

Voici un autre gag dû à René Goscinny :
Les casques et les armures fortement cabossés, des légionnaires romains font l'addition suivante à leur supérieur :
"- Ave centurion ! Nous avons été attaqués par une troupe gauloise très supérieure en nombre !
- Donnez moi leur signalement !
- Ben, un gros et un petit, et un petit chien, et ils portaient chacun un sanglier sur le dos.
- Ils étaient cinq, quoi !"

Un peu de réflexion. OK pour compter les deux guerriers gaulois comme un seul ensemble. Il arrive, avec bien des si et des mais, qu'un canidé fasse équipe avec des humains dans le combat. En pareil cas, oui on pourrait compter trois combattants. Avec des acrobaties intellectuelles douteuses, on pourrait mettre ensemble les deux suidés morts et le canidé vivant : tous trois dégagent une odeur de fauve, peut-être ? Ou tous trois pourraient servir de repas à une famille d'ours, ou à une meute de loups. Mais les compter tous les cinq comme "une troupe gauloise très supérieure en nombre" ? Heu... Vous êtes sûrs que ce soit là un ensemble pourvu de cohérence ? Avec une relation d'équivalence entre ses cinq éléments ?

En revanche, ils pourraient être ensevelis tous les cinq par un glissement de terrain ou une avalanche, et leurs ossements être démêlés longtemps après par une même équipe d'archéologues ou de paléontologues.

Flous et erreurs irréductibles

Enfin, il est fréquent qu'une collection ne soit définie qu'avec un flou irréductible. Chose impensable pour un nombre pur.

Prenons l'exemple de la population de la France : à tout instant, il meurt des gens, il naît des bébés, des gens entrent, d'autres sortent. D'autres disparaissent, d'autres entrent subrepticement, des agents clandestins emprunteront plusieurs identités tour à tour... Pendant ce temps là, compter les gens prends du temps de recenseurs, qui ne peuvent être partout.
Quelles que soient les précautions méthodologiques prises lors du recensement, il subsiste des marges d'erreurs et d'incertitudes irréductibles, et ces marges d'erreurs dépendent des méthodes et des moyens du comptage. Nous sommes donc contraints de distinguer plusieurs étages dans les abstractions à partir de la réalité complexe et partiellement insaisissable de la population du pays.

Inscription dans un un schème d'abstractions normalisables interprofessionnelles

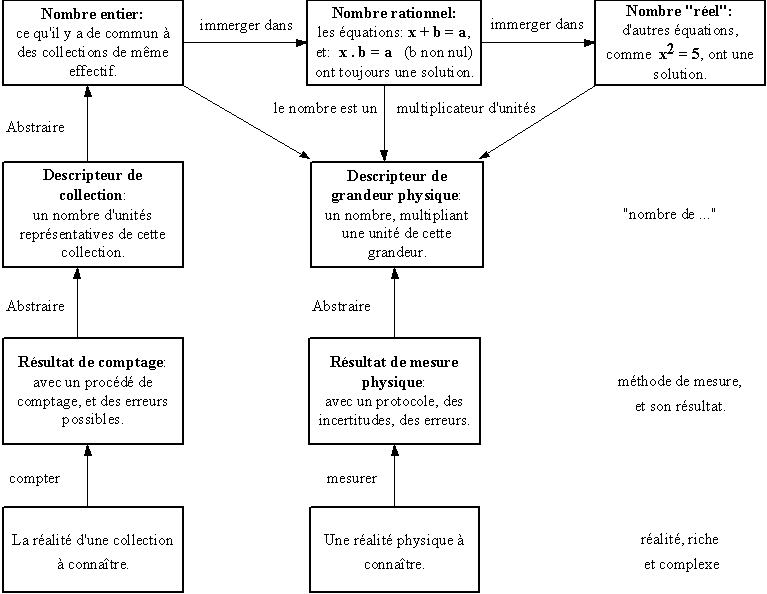
Les grandeurs physiques sont semi-abstraites, et gardent une propriété du monde réel, dont les nombres sont dispensés : une signification, une unité-étalon, et la grammaire de variance qui y est associée.

Les grandeurs physiques sont dispensées des propriétés fort compliquées des mesures, et des résultats de mesures (avec toutes leurs sortes d'incertitudes et d'erreurs), et de celles du stockage de ce résultat sur un papier ou dans une machine électronique, avec ses problèmes de largeur et de résolution limitées.

Pour les grandeurs concrètes et les grandeurs physiques, l'égalité a un sens, si l'on sait définir un protocole de comparaison et de mesure. Par exemple, comparer deux longueurs, comparer deux aires, ou comparer deux lots de paquets de lessive, sous fardelages différents. A ce prix, nous avons le droit d'écrire une égalité de grandeurs, même en unités inhomogènes, comme :

1 tour = 2 radians.

La grandeur physique est définie comme l'abstraction commune à ce qui dans la réalité est justifiable de la même famille de protocoles de mesure, dont la précision et le coût peuvent être très différents, mais qui ont tous pour objet de comparer une même sorte de grandeur. Par exemple une longueur, ou une masse au repos.

C'est donc aussi une classe d'équivalence. Elle est bien moins abstraite qu'un nombre, car elle est un descripteur de quelque chose. Elle est tenue à la syntaxe inhérente à la vocation sémantique de chaque grandeur physique.

Nous allons avoir besoin de caractériser ces grandeurs pratiques et concrètes d'une part (par exemple 500 flacons d'un médicament), et ces grandeurs physiques d'autre part, par leur lien avec une grandeur unité, et avec l'ensemble des nombres réels. Nous allons donc définir les grandeurs scalables. Nous aurons aussi besoin de distinguer entre les grandeurs arbitrairement scalables, et les grandeurs nombrables, pour lesquelles existe une unité absolue définie par la nature, et non par une simple convention dans société humaine.

En 1873, James Clerk Maxwell consacrait le premier paragraphe de son Treatise (Clerk Maxwell 1873) à expliquer que toutes les grandeurs physiques sont le produit d'un nombre par un échantillon de cette grandeur, appelé unité.

Prenons la largeur de cette feuille de papier, qui sort de mon imprimante. Elle mesure 21 cm; ou 210 mm; ou 0,21 m. Or, il n'existe aucune fonction à valeur de nombre réel ayant la propriété que : 21 = 210 = 0,21.

Tandis qu'il est parfaitement correct d'écrire que : 21 cm = 210 mm = 0,21 m.

Ces deux égalités ne sont pas écrites entre nombres, mais entre grandeurs physiques. Elle dénotent des classes d'équivalences déterminées par les principes des mesures. Ici, seuls les principes d'au moins un protocole de mesure des longueurs, au moins un principe de construction des appareils de mesure, et des campagnes de mesures vérifiant l'équivalence et la bonne adéquation de ces appareils et de ces protocoles, peuvent justifier la définition de la grandeur physique, et les conditions de l'égalité.

Une distinction sera utile par la suite :

1. Une grandeur est dite nombrable si elle est par nature multiple entière d'une unité donnée par la nature.
   Aux naissances près, et à la croissance près des poulains, l'effectif d'une harde de chevaux est nombrable. Une charge électrique est toujours multiple entière (éventuellement fluctuante) de la charge élémentaire d'un électron ou d'un proton, c'est donc une grandeur nombrable. Les nombres baryoniques, ou nombre de nucléons dans la matière, sont aussi des grandeurs nombrables. Dans les entrepôts, les nombres de cartons de telle marchandise, sont par excellence nombrables, et les cachets dans une boîte de médicament aussi. Bien sûr, nous considérons un cachet de médicament, une boîte de 30 cachets, et un carton normalisé de ces médicaments, comme des unités naturelles, aussitôt qu'ils sont fabriqués. Ce sont bien des objets concrets, qui s'imposent comme tels au comptable ou au magasinier.
2. Une grandeur est arbitrairement scalable, ou en abrégé "scalable", si le choix de l'unité physique est laissé à un arbitraire humain. Ainsi les tensions électriques, les intensités du courant électrique, les masses, les longueurs, les durées, etc. dont les étalons sont dûs à des décisions humaines, aussi nécessaires qu'arbitraires.
   Soit la majorité des grandeurs physiques dont s'occupe le physicien, à la limite toutes les grandeurs macroscopiques tant qu'on est très loin de la limite atomique.

Cinq règles d'usage pouvant servir d'axiomes :

1. On ne peut additionner (ou retrancher) que des grandeurs de même nature. Encore faut-il qu'elles soient des grandeurs extensives. Pour les grandeurs intensives, ce peut être exclu, cas de la température par exemple, ou restreint à des dispositions expérimentales contraignantes.
2. On peut multiplier une grandeur physique nombrable par n'importe quel nombre entier. On peut multiplier une grandeur physique arbitrairement scalable par n'importe quel nombre réel.
3. Dans la famille des grandeurs physiques, écrire une égalité, suppose qu'on a réussi à définir une méthode expérimentale, et des instruments, pour comparer.
   On a alors le droit d'écrire une égalité entre grandeurs, comme 210 mm = 21 cm. Nous exprimons la grandeur physique comme le produit d'un nombre, par une unité de cette grandeur. Il faut avoir défini ou construit un étalon de cette grandeur-unité.
4. Toute grandeur physique a un inverse, et il n'est pas nécessaire de définir à nouveau une méthode de mesure. Exemples : un décamètre est gradué à 100 divisions par mètre. L'inverse du mètre s'écrit m^-1.
5. On est libres de multiplier une grandeur physique par n'importe quelle autre grandeur physique; ou de diviser par une grandeur physique non nulle. Cette opération est externe : elle génère une autre grandeur physique distincte.

Savoir si le résultat a un intérêt pratique, n'est que la question suivante. On peut montrer que les résultats réellement pratiques forment une structure assez simple et remarquable.

Enfin ces propriétés bien agréables de linéarité ne sont valides que dans un espace comparable au nôtre : faible gravité, états gazeux ou modérément condensés, températures modérées. Dans une étoile à neutrons, notre physique familière aurait beaucoup de surprises.

L'analyse dimensionnelle, premier garde-fous du physicien.

Dès le 17e siècle, Marin Mersenne faisait un usage judicieux et fécond de l'analyse dimensionnelle.

Reprenons son exemple, mais avec le système d'unités moderne MKSA : de quoi dépend la période d'un pendule pesant ?

Le pendule pesant se caractérise par l'accélération de la pesanteur là où il est, uniforme à l'échelle des mouvements du pendule, sa masse, la distance du centre de gravité à l'axe de suspension ou au point de suspension, et l'angle maximal des oscillations (angle pris par la tige par rapport à la verticale, si pendule simple).
Gravité g : L. T^-2,
Masse m : M,
Longueur a : L,
Période T : T.

Il n'y a qu'une seule combinaison (valide aux petits angles) qui donne la bonne dimension, des secondes :
T = {coefficient numérique} *
Il ne reste plus qu'à déterminer si le coefficient numérique est 1, ou , ou l'inverse, . Cela dépend essentiellement de l'unité d'angle du problème : radians ou cycles. Ici, il faut remonter à l'équation du mouvement, en approximant l'énergie potentielle au premier terme de son développement limité :
m.g.h = m.g.a.
où l'angle est en radians.
On écrit que l'énergie mécanique est constante, donc sa dérivée est nulle, d'où il résulte que le carré de la pulsation est .
D'où le coefficient pour la période :

La masse ne joue aucun rôle dans la formule.

La variance des grandeurs scalables

Par définition, on peut les rapporter à une unité : elles sont le produit d'une grandeur-unité par un nombre réel.

Par conséquent, si l'on change l'unité de mesure d'une grandeur scalable, le quotient de cette grandeur (par exemple un prix) par son unité est contravariant à cette unité. Dans les classes primaires, ce nombre quotient est désigné comme "le nombre exprimant la mesure de ...", ce qui est trop lourd. Dans les espaces de dimension supérieure à 1, chacun de ces quotients, serait désigné comme "coordonnée", ce qui ici, serait prématuré. Il faut trouver mieux pour ce stade. Je suggère : "multiplicateur", ou "quotient".

Exemples : On peut s'acquitter d'une dette de mille francs, avec deux billets de 500 F, ou vingt billets de 50 F. On peut expédier 60 tonnes de marchandises, par 3 camions de 20 tonnes, ou par 2 camions de 30 tonnes. Cette page mesure en large 21 cm, ou 210 mm, ou 0,21 m. 21 cm = 0,21 m : le quotient est contravariant au diviseur. Quand l'unité est 100 fois plus grande, alors le quotient (de la grandeur par l'unité de base) est 100 fois plus petit. Autrement dit, les quotient varient au contraire de l'unité de base, afin d'avoir compétence à désigner la même grandeur.

Schéma : Grandeur scalable = quotient * grandeur-unité.

Et si l'unité est composée ? Si l'essence est à 5,60 F le litre, et que le dollar est à 5,60 F, alors l'essence est à 1$ le litre : contravariance. Mais elle est à 3,785 $ par gallon, ou encore à 21,20 F par gallon, puisqu'un gallon vaut 3.785 litres : covariance. Ce prix par unité de volume, varie comme l'unité de volume.

Le nombre qui exprime ce prix de l'essence, est covariant à l'unité de capacité : il grandit ou rapetisse comme elle. Ce nombre est contravariant à l'unité monétaire : il grandit ou rapetisse à l'envers de l'unité monétaire. Bizarrement, ces mots de covariance et de contravariance, n'étaient entendus qu'en fin d'études supérieures, alors que les phénomènes désignés, sont rencontrés dès les classes primaires. Rencontrés, mais ignorés dès le passage dans l'enseignement secondaire. C'est une lacune regrettable, car les notions de variance sont le coeur même de la mesure et de la physique. Cette syntaxe des unités physiques, a presque toujours été sous-estimée. Les mathématiciens n'ont jamais daigné s'y intéresser, et trop de physiciens sont trop inadvertants pour en tirer toutes les conséquences.

En grandeurs physiques, les conversions d'unités coulent de source

Calcul d'une longueur d'onde : "Longueur d'onde" = "célérité" . "période"
Les autres combinaisons possibles, que bien de nos élèves lancent au hasard, ne donneront jamais des mètres.
L = L/T . T

"Longueur d'onde" = 343 m/s . 0,025 s = 343 . 0,025 s.m/s = 343 . 0,025 m = 8,6 m

Toutes les conversions d'unités coulent alors de source. On s'impose de n'écrire que des égalités vraies en grandeurs physiques.
Par exemple, pour traduire une masse volumique (ici celle d'un acier) donnée dans des unités non S.I., vers le Système International, on commence par écrire la tautologie :

7,8 . = 7,8 .
Jusqu'ici, on n'a certainement violé ni la physique, ni la mathématique.

Puis on multiplie le second membre par une fraction égale à 1. On la choisit de façon à faire apparaître les éléments d'unités voulus, et faire disparaître, par simplification, les éléments d'unités indésirables. Ici on veut faire disparaître grammes du numérateur, et y faire apparaître kilogrammes, faire disparaître cm3 du dénominateur, y faire apparaître m3. Procédons en deux étapes :

7,8 . = 7,8 . . . = 7,8.
(commutativité nombre.unité)

7,8. = 7,8. = 7800 .

Aux élèves doués, la méthode peut paraître lourde, peu valorisante, et socialement peu sélective. Ils préfèrent deviner le bon résultat, au flair. Mais tous les autres élèves préfèrent cette méthode : elle est incassable !

Mettre en équations, garde-fous par les unités et l'analyse dimensionnelle.

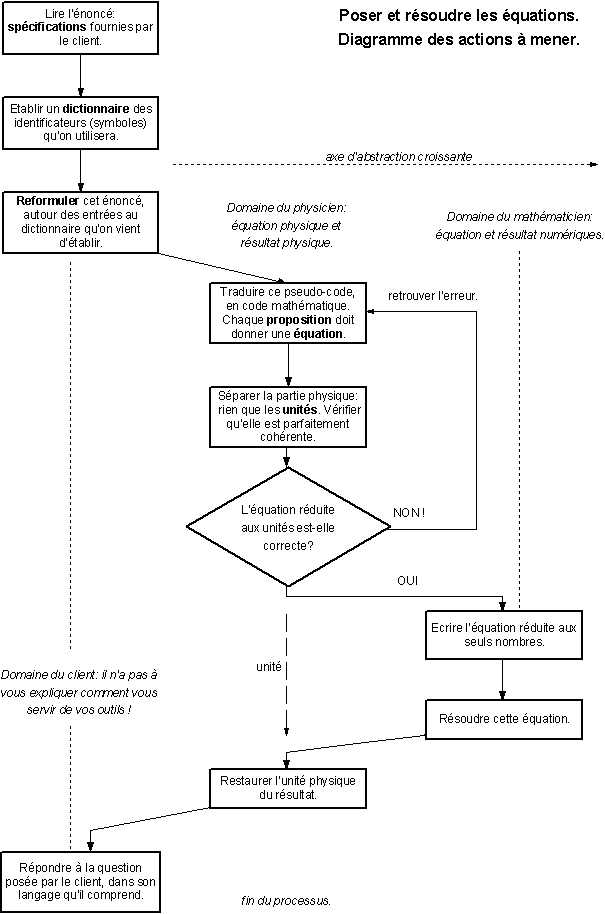
Voici le schéma ci-après, donné en classe, des deux étages d’abstraction dans la résolution d’un problème par l’algèbre.

· Première abstraction : du problème formulé par le client, vers une schématisation des phrases d’énoncé, l’écriture d’un dictionnaire des variables et de leurs symboles (que ce dictionnaire ait une, deux ou dix entrées) et la transcription par la pose d’un système d’équations.

· · Seconde abstraction, quand la vérification dimensionnelle est terminée et ne révèle plus d’erreurs, alors résoudre le sous-système numérique, par les méthodes algébriques.

· · Seconde désabstraction : restituer les unités physiques, pour répondre en grandeurs physiques au problème physique.

· Première désabstraction : répondre dans le langage du client, dans des termes qui lui sont accessibles, et qui répondent à son problème.

Opérateurs de proportionnalité

Si je commande un tissu au mètre, et que le prix du mètre est de 3,90 euros, l'opérateur de proportionnalité qui transforme les mètres en prix du coupon, est "multiplier par 3,9 €/m".

S'agissant d'un envoi par la poste ou un transporteur, le vendeur ajoute un frais d'expédition, que pour simplifier, nous allons considérer fixe, à dix euros.
Soit un nouvel opérateur "Ajouter 10 €".

On peut inverser cette opération, pour répondre à la question : "J'ai tel budget. Quel métrage de ce tissu puis-je acheter ?".
Cela donne la successions d'opérations suivantes :
Retrancher dix euros au budget.
Diviser par le prix du mètre.
Prendre la partie entière de ce résultat en mètres : le vendeur ne compte que des mètres entiers.

L'opérateur demi-tour

L'examen de la littérature scientifique du 18e et du 19e siècle, par exemple l'article écrit par Jean le Rond d'Alembert pour l'Encyclopédie, "Nombres négatifs" met en évidence les difficultés nées de la confusion entre nombres et opérateurs. La notion de nombre, triomphante depuis l'Antiquité avec Pythagoras, dévorait celle d'opérateur. D'Alembert concédait que les règles de calcul sur les nombres négatifs étaient correctes, tout en maintenant qu'ils étaient embarrassés sur leur interprétation. Que -1 soit un nombre, pourquoi pas ? Mais ce qui est sûr, c'est que multiplier par -1 est un opérateur.

Beaucoup de nos élèves perdent pied à ce moment là : personne n'avait pensé à leur donner d'image ni d'application parlante, de référence concrète pour ces opérateurs, ni leur champ d'application.

Prenant de ces paumés en B.E.P., je rattrapais leur retard en posant le support, une droite orientée, un de ces axes où l'on pose des abscisses, pour peu qu'on ait défini un vecteur unité dessus. Une parenthèse, je leur donnais l'image d'un autobus miniature, ou d'un wagon miniature, avec des voyageurs dedans. Multiplier cette parenthèse par -1, revenait à retourner le wagon (et ses passagers inclusivement). Multiplier deux fois par -1, c'était faire deux fois un demi-tour, soit revenir à l'orientation initiale.

Nous y reviendrons, avec l'opérateur quart-de-tour, applicable à des vecteurs.

Liens vers les chapitres suivants, grandeurs géométriques de la physique

Vecteurs, définition, propriétés
Métrique des grandeurs vectorielles en physique
Les quart-de-tours entre vecteurs : gyreurs

Bibliographie et Références

APMEP, Commission Mots, n° 6 : Grandeurs et mesures. APMEP, 1982, Paris. Brochure n° 46.

André Pressiat. Calculer avec les grandeurs Actes de l'Université d'été de Saint-Flour.

André Pressiat. Quotients - Proportionnalité - Grandeurs Quotients - Proportionnalité - Grandeurs

Jean-François MUGNİER. Recherche et rédaction de problèmes au Collège. Feuille de Vigne n° 100 – Juin 2006.