Calcul des coordonnées de gyreur vitesse angulaire
Calcul rigoureux (mais trop compliqué) pour le cas du gyreur strict, quotient
Le lecteur peut sauter ce paragraphe, et aller directement au suivant.
Feignons d'ignorer tout du calcul matriciel, des représentations matricielles, mais en sachant tout de même la trigonométrie.
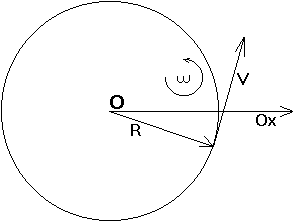
Désignons par l'angle (quelconque) de
avec l'axe des x. Alors les coordonnées de
sont R cos
, et R sin
(et zéro, si l'on s'encombre dès maintenant de la 3e dimension).
Tandis que les coordonnées de sont : V cos(
+
/2) et V sin (
+
/2)
(signe +, car rotation dans le sens direct, pour des axes orientés de même). Exprimons les quatre quotients.
Mimant l'ignorance totale, nous allons même ignorer qu'il est plus pratique de les ranger en tableau carré. Rangeons donc provisoirement en ligne les quatre influences-d'une-coordonnée-de-R-sur-une-coordonnée-de-V (les signes affectant des valeurs absolues, dépendent évidemment du signe de la rotation, par rapport à l'orientation des axes de coordonnées) :
| de Rx vers Vx | de Rx vers Vy | de Ry vers Vx | de Ry vers Vy |
|---|---|---|---|
| V/R tg |
V/R | -V/R | V/R cotg |
Premier mouvement de panique : Ces coefficients sont trop compliqués ! Mais remarquons que ces coefficients sont deux à deux redondants, et que si nous les appliquons simultanément, nous obtiendrons à chaque instant le double de la vitesse .
Vx = ½ V/R (+ Rx tg - Ry )
Vy = ½ V/R (+ Rx + Ry cotg
Nous avons intérêt à scinder ces coefficients en deux groupes, dont chacun est suffisant :
| de Rx vers Vx | de Rx vers Vy | de Ry vers Vx | de Ry vers Vy |
|---|---|---|---|
| 0 | V/R | -V/R | 0 |
| V/R tg |
0 | 0 | V/R cotg |
Or, seul le groupe de la première ligne a la propriété d'être invariant envers . Lui seul donc est digne de représenter l'être physique "vitesse angulaire de rotation", qui lui, est un invariant quel que soit
. Le second groupe conviendrait pour décrire une oscillation harmonique droite. Ici ce n'est qu'une fausse solution, proposée par notre mathématisation : un groupe non faux, mais sans intérêt, et affligé de discontinuités rédhibitoires pour
=
/2 + k
. Une autre façon équivalente, d'apparence plus rigoureuse, est de faire la moyenne des coefficients trouvés, en faisant varier
de 0 à 2
. Les termes en tg
et cotg
s'annulent en moyenne. Ce qu'il fallait démontrer. Il ne reste plus au lecteur, qu'à se convaincre de l'intérêt de disposer ces quatre coefficients retenus, sous la forme d'un tableau carré, au lieu de les entasser en ligne.
Calcul simplifié
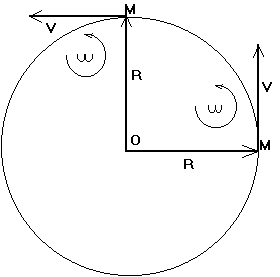
Il nous suffit de sélectionner deux positions du vecteur
Il est judicieux de prendre deux positions orthogonales entre elles : successivement selon l'axe Ox, puis selon l'axe Oy, et de résoudre le système de 2 équations. On pose les vecteurs sous forme colonne.
R11 = R
R12 = 0 (1ère coordonnée du 2e vecteur)
R21 = 0 (2ème coordonnée du 1er vecteur)
R22 = R
V11 = 0
V12 = -V (1ère coordonnée du 2e vecteur)
V21 = V (2ème coordonnée du 1er vecteur)
V22 = 0
On résout le système suivant, où les coordonnées de sont les inconnues :
(produit matriciel, ordinaire)
D'où la solution : (coordonnées de
On remarque qu'en repère orthonormal, les coordonnées mixtes se comportent comme des coordonnées homogènes, et sont sagement antisymétriques. Il ne reste bien qu'une seule coordonnée stricte non nulle. En repère non orthonormal, il faut revenir à la discipline de base, et n'antisymétriser que des coordonnées homogènes : entièrement covariantes, ou entièrement contravariantes. Nous y reviendrons. Mais attention à un oubli qui pourrait nous coûter cher ultérieurement : le gyreur ne caractérise la rotation que du seul point de vue différentiel. A lui seul, il perd une constante d'intégration capitale : le sous-espace invariant. C'est à dire le centre de rotation dans le plan, ou l'axe de rotation dans l'espace R3. Souvenons-nous en quand nous étudierons le moment angulaire.