Propagation des fermions
Sommaire
Un sottisier à déblayer au préalable
Présenter l'optique incohérente pour de la cohérente
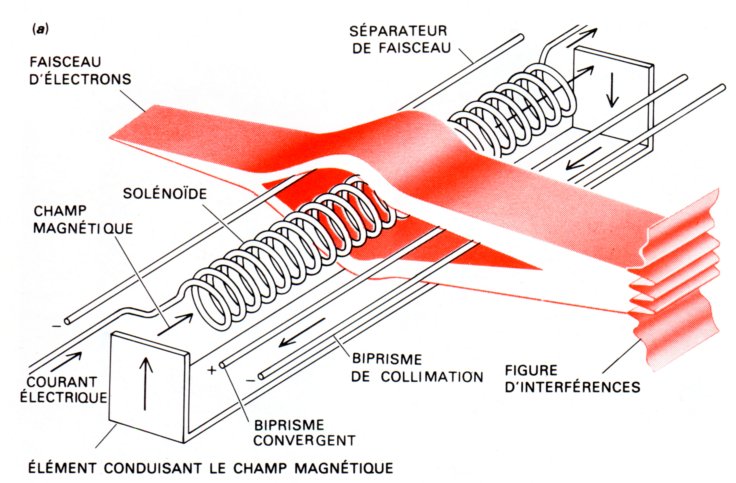
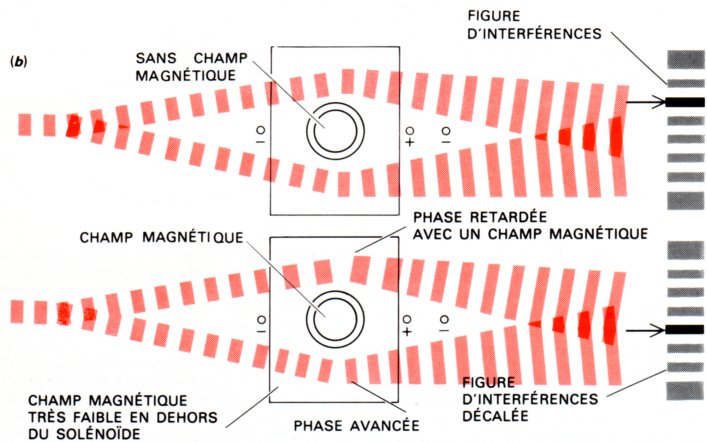
Le compte-rendu d'une au moins des réalisations de l'expérience proposée par Aharanov et Bohm en 1959, figure en pages 156 à 159 de "Les particules élémentaires", Editions Pour la Science et Belin, 1986, par Herbert Bernstein, et Anthony Phillips.
Ils écrivent que : "La phase globale d'un faisceau d'électrons qui n'est soumis à aucune interaction n'a aucun effet sur les quantités observables, mais la différence de phase de deux faisceaux partiels qui arrivent en un même point de l'espace a une réalité physique. La différence de phase entre deux faisceaux qui interfèrent agit sur la hauteur maximale de l'onde de l'électron et elle change donc l'amplitude de probabilité.
...
Par conséquent quand deux faisceaux se rencontrent, on observe une figure d'interférence."
Passons sur "hauteur", qui n'est probablement dû qu'au traducteur anonyme. Il présente l'onde comme scalaire, alors qu'elle est bispinorielle, à quatre composantes.
L'erreur de base qui est dictée au lecteur, est qu'un faisceau d'électrons, dont les vitesses sont dispersées, et qui aboutissent tous en des absorbeurs différents, auraient quand même une phase unique, partagée. C'est une absurdité de gros calibre.
Or l'unicité de vitesse du faisceau n'est qu'approximative : la source d'électrons demeure un filament chauffé, comme dans n'importe quel téléviseur ou oscilloscope cathodique. Ils ont donc tous aussi des vitesses de phase différentes. Ils sont émis de façon asynchrone et aléatoire par la source thermo-électronique. Certes des photons, parcourant ensemble des espaces astronomiques, ont tendance à se synchroniser en phase, ce qui permet l'astronomie par interférométrie à large base... Mais là nous sommes sur des dimensions internes à un microscope électronique, et de plus ce sont des fermions. Aucune espèce de coopération de phase, donc. C'est une source incohérente.
Bref, nos deux auteurs ont complètement oublié ce qu'on nous avait appris en terminale (en 1962 pour moi) : en optique nécessairement incohérente, chaque électron interfère avec lui-même, et avec rien ni personne d'autre. Donc chaque électron passe simultanément au dessus et en dessous du solénoïde et des trois fils chargés, qui font l'optique de partage et de refocalisation. Ce qui bien sûr cadre fort mal avec le dogme seriné par ailleurs, que les électrons seraient "ponctuels", tout en omettant de définir ce mot - qui pourtant pose un grave problème de définition.
Les deux figures ci-dessus, seraient dues à George G. Kelvin.
"fréquence proportionnelle à l'énergie". Oui mais laquelle ?
Même page 156 du même article, on relève l'explication suivante :
"On peut représenter un électron du faisceau par une onde dont la longueur d'onde est inversement proportionnelle à la quantité de mouvement de l'électron, et dont la fréquence est proportionnelle à son énergie.
Oui, mais laquelle au juste, de "son énergie" ? Relativiste, ou non relativiste ? Si c'est non relativiste, alors implicitement un électron au repos aurait un fréquence nulle. Et quant à la vitesse de phase ?
Rappelons comment l'entourloupe a été réalisée ; c'est assez croquignolet.
Dans sa thèse, Louis de Broglie écrit :
« On peut donc concevoir que par suite d’une grande loi de la Nature, à chaque morceau d’énergie de masse propre m, soit lié un phénomène périodique de fréquence telle que l’on ait :
,
étant mesurée, bien entendu, dans le système lié au morceau d’énergie. Cette hypothèse est la base de notre système ... » (thèse de 1924)
Plus loin dans son travail, il explique ce qui lui fait penser que ce phénomène périodique n'a pas lieu d'être considéré a priori comme confiné : il s'agirait donc d'une onde se propageant dans l'espace.
La masse m étant la masse au repos de la particule, pour être cohérent avec la définition donnée de la masse ci-dessus, on doit écrire
L'hypothèse de l'harmonie des phases ayant conduit, au paragraphe précédent, à l'expression (cf p 35 de sa thèse, où il l'écrit V=c/β). La longueur d’onde étant le rapport de la vitesse de phase V à la fréquence
, on a :
En utilisant la quantité de mouvement :
on obtient la relation relativiste de Broglie :
Relation que l'on peut conserver même après éradication et de Louis de Broglie, et de la fréquence intrinsèque qui est à la base de tout.
Après ce nettoyage ethnique, il subsiste une longueur d'onde, observée, connue de tous, qui est en même temps le quotient d'une vitesse de phase inconnue, par une fréquence inconnue... "Inconnues", au sens orwellien, de "passées au Trou de Mémoire".
Equation de Dirac (rédaction en cours)
L'équation de Dirac est une équation formulée par Paul Dirac en 1928 dans le cadre de sa mécanique quantique relativiste de l'électron. Il s'agit au départ d'une tentative pour incorporer la relativité restreinte à des modèles quantiques, avec une écriture linéaire entre la masse et l'impulsion.
Cette rédaction est en cours depuis une ébauche.
Le but est de donner la description de la propagation, en clair, et avec la progression des fronts d'ondes. La mission est de prouver que ça ne peut qu'osciller.
Explication
Cette équation décrit le comportement de particules élémentaires de spins demi-entiers, comme les électrons. Dirac cherchait à transformer l'équation de Schrödinger afin de la rendre invariante par l'action du groupe de Lorentz, en d'autre termes à la rendre compatible avec les principes de la relativité restreinte.
Cette équation prend en compte de manière naturelle la notion de spin introduite peu de temps avant et permit de prédire l'existence des antiparticules. En effet, outre la solution correspondant à l'électron, il découvre une nouvelle solution correspondant à une particule d'énergie négative et de charge opposée à celle de l'électron.
En 1932 Carl Anderson, alors qu'il étudiait des photons de haute énergie en provenance de l'espace, constate que l'interaction de ces photons avec la chambre à brouillard produit une particule qui s'identifie à la particule conjecturée par Dirac, le positron.
Problèmes d'horizons de validité
Ainsi qu'il est d'usage à cette époque, P.A.M. Dirac utilisait les coordonnées de temps et d'espace comme si elles étaient valides à l'échelle de l'électron. Or cette extension de validité n'a jamais été prouvée expérimentalement. Il faudra y revenir, car c'est une question centrale en microphysique.
Formulation mathématique
Sa formulation exacte est :
où m est la masse de la particule, c la vitesse de la lumière, la constante de Planck réduite, x et t les coordonnées dans l'espace et dans le temps, et ψ(x, t) une fonction d'onde à quatre composantes. (La fonction d'onde doit être formulée par un spineur à quatre composants, plutôt que par un simple scalaire, du fait des exigences de la relativité restreinte.) Enfin
sont des matrices de dimension
agissant sur le spineur
et appelées matrices de Dirac. En termes des matrices de Pauli
on peut écrire les matrices de Dirac, dans la représentation de Dirac (d'autres sont possibles, comme la représentation de Weyl ou la représentation de Majorana), sous la forme
Il est commun en mécanique quantique de considérer l'opérateur quantité de mouvement et dans ce cas l'équation de Dirac se réécrit de façon condensée
De plus, il est naturel de chercher une formulation covariante, ce qu'on fait en posant et
, auquel cas on a (en adoptant les conventions c=1 et
) une notation encore plus compacte :
où l'on a adopté la notation de Feynman
Formulation mathématique en pulsation
Il est utile, mais peu pratiqué, de procéder à un peu d'analyse dimensionnelle, pour faire apparaître la pulsation et la phase de cette onde.
En effet , fréquence broglienne, en cycles par seconde,
ou encore , pulsation broglienne, en radians par seconde.
Ecriture développée
Cette partie est à remanier : les matrices de Pauli dépendent d'un choix sur la direction "de quantization", c'est à dire en clair d'interaction de nature gyratorielle, interaction magnétique ou de moment angulaire. La première rédaction n'en tenait pas compte, faisait comme s'il y avait une symétrie, et c'est une erreur.
Il est possible de résoudre les opérations matricielles, ce qui donne :
Après a-dimensionnalisation la plus poussée possible grâce à la pulsation broglienne :
Il est intéressant de mettre en évidence une symétrie du genre relativiste entre les dérivations par rapport aux quatre coordonnées d'espace-temps :
La suite de votre mission consiste à exprimer ces coefficients imaginaires comme des déphasages de l'onde, soit temporels, soit spatiaux.
Matrices de Dirac
Les matrices de Dirac sont des matrices qui furent introduites par Paul Adrien Maurice Dirac, lors de la recherche d'une équation d'onde relativiste de l'électron.
Intérêt
La généralisation naturelle de l'équation de Schrödinger est l'équation de Klein-Gordon.
où représente l'opérateur d'alembertien :
On peut également utiliser le formalisme relativiste (en unités naturelles) :
avec les conventions :
Malheureusement, celle-ci décrit des particules de spin 0 et ne convient pas pour les électrons qui sont de spin 1/2. Dirac essaya alors de trouver une équation linéaire comme celle de Schrödinger sous la forme :
où est une fonction d'onde vectorielle,
la masse de la particule,
l'hamiltonien et
sont respectivement un vecteur de matrices hermitiques et une matrice hermitique. L'équation de Dirac doit respecter les trois points suivants :
- Les composantes de
doivent satisfaire l'équation de Klein-Gordon, une onde plane dont une solution est :
-
- Il existe un quadrivecteur densité de courant qui est conservé et dont la composante temporelle est une densité positive (identifiée avec la charge électrique).
- Les composantes de
ne doivent satisfaire aucune condition auxiliaire, c’est-à-dire qu'à un instant donné elles sont des fonctions indépendantes de
.
Matrices de Dirac
Dirac proposa que les matrices hermitiques soient anticommutantes et de carré égal à un. C’est-à-dire qu'elles obéissent à l'algèbre suivante :
où les crochets sont l'anticommutateur .
En élevant l'équation de Dirac au carré, on vérifie immédiatement que la première condition est satisfaite. On introduit ensuite les matrices de Dirac proprement dites :
Le slash de Feynman
On introduit aussi le « slash » de Feynman :
L'équation de Dirac prend alors la forme :
Une représentation explicite, dite « représentation standard », est donnée par :
où est la matrice unité 2×2 et
sont les matrices de Pauli.
Cette représentation est particulièrement pratique car elle met en évidence le caractère spinoriel (dû au spin demi-entier) de la fonction d'onde de l'électron et elle sépare les composantes d'énergie positive et négative. Ainsi, en écrivant la fonction d'onde comme un bispineur :
où et
sont deux spineurs, l'équation de Dirac devient :
En introduisant la fonction d'onde conjuguée comme :
On trouve :
Et avec l'équation de Dirac, cela donne :
Ce qui donne un courant conservé :
Dont la composante temporelle est positive. On définit aussi la matrice :
L'utilisation de permet ainsi de construire différents types de combinaisons tel que :
des vecteurs :
des pseudovecteurs :
des scalaires :
des pseudoscalaires :
On vérifie aisément la covariance relativiste de tout ce formalisme.
Représentations
Les matrices de Dirac sont totalement déterminées par la relation :
où est le tenseur de Minkowski. On a aussi
.
Il existe une infinité de solutions possibles à la relation précédente. Pour des matrices 4×4, l'ensemble des solutions est une algèbre de dimension 4, une algèbre de Clifford notée
, et les quatre matrices de Dirac en forment une base. Suivant la base choisie les matrices de Dirac ont des coefficients différents, et ce choix s'appelle une représentation des matrices de Dirac.
Représentation de Dirac
C'est la « représentation standard ». On l'obtient à partir de la représentation de Weyl grâce à l'opérateur unitaire U :
Les matrices s'écrivent alors :
Représentation de Weyl
Représentation qui tombe "naturellement" quand on cherche à dériver l'équation de Dirac à l'aide des représentations irréductibles du groupe de Lorentz. Dans cette base, les matrices ont la forme suivante :
Représentation de Majorana
La représentation de Majorana est obtenue à partir de la « représentation standard » à l'aide de la matrice unitaire U suivante :
Cette représentation a la propriété intéressante que toutes les matrices sont imaginaires pures, ce qui rend les calculs commodes quand on considère l'opérateur conjugaison de charge.
Représentation chirale
Son avantage est que les deux spineurs se transforment indépendamment sous les rotations et les translations. Elle est particulièrement utile pour des particules sans masse, les équations se simplifiant considérablement. Elle a été utilisée pour le neutrino bien que l'on sache maintenant que celui-ci possède une masse extrêmement petite mais non nulle.
Tremblement de Schrödinger
Rédaction en cours...