Un échec pédagogique sanglant : comment les autres professions, utilisatrices de mécanique, et les vulgarisateurs enseignent Coriolis et ses effets en océanographie et en météorologie.
Voyons un exemple éduqué, par quelqu'un qui a fait des études supérieures :
http://archimer.ifremer.fr/doc/1960/publication-4282.pdfNous savons en effet que. d'une façon générale, un courant qui passe sur un haut fond augmente de vitesse en s'infléchissant vers la droite sous l'effet de l'accélération de Coriolis, tandis que sa vitesse diminue au-dessus des plus grands fonds, le mouvement étant alors dévié vers la gauche.
Si ça c'est ce qu'écrit un scientifique formé, mais pas à la mécanique, alors mieux vaut vous passer sous silence les torrents d'insultes et d'inepties que nous lancent les populistes ignorants, c'est à vomir. Revenons aux affirmations de ce Charles Allain.
Précisons qu'il s'agit des courants en Méditerranée, donc il est acquis que c'est entièrement dans l'hémisphère Nord.
L'affirmation "
le courant est dévié vers la gauche en passant sur les grandes profondeurs" est juste fausse, contrafactuelle.
Mais l'affirmation précédente, qu'un courant s'infléchisse vers la droite
sous l'effet de l'accélération de Coriolis est contradictoire avec les définitions, et est caractéristique d'un enseignement de la mécanique sous monopole de matheux, qui
crassussent (recopient)
bovinement les errements du plus ancien dans le grade le plus élevé, qui lui-même les tenait de, etc.
L'accélération de Coriolis, c'est celle qu'une liaison de guidage impose à un mobile pour qu'il ne suive pas une trajectoire inertielle, mais demeure sur une trajectoire orthodromique, celle qui semblait irréprochable à l'observateur qui ignore que la Terre tourne, et n'est donc pas un repère galiléen.
Tandis qu'une trajectoire inertielle échappe au contraire à l'accélération de Coriolis, et s'infléchit par rapport à l'orthodromie terrestre : elle s'infléchit en tournant non pas comme la Terre par rapport au ciel, mais comme la voûte céleste par rapport à la Terre. Tel est le cas d'une chute libre à l'équateur : il y a conservation de la composante Est de la quantité de mouvement, mais diminution du rayon de giration, donc augmentation de la vitesse angulaire et déviation vers l'Est, à l'Est de la verticale locale statique. La courbure de la trajectoire apparente (terrestre) du mobile est conforme à celle de la trajectoire apparente des étoiles pour l'observateur terrestre.
Les matheux n'aident pas quand ils donnent la formule avec deux produits "vectoriels", où par deux fois intervient une convention arbitraire et anti-physique, genre :
l'accélération de Coriolis : [tex]2\vec{\Omega}\wedge\frac{\delta\vec{r}}{\delta t} [/tex]
Le grand public sait dans quel sens tourne la Terre par rapport au ciel, mais ignore si les matheux qui remplacent cet être de rotation par un être vectoriel, font pointer le dit vecteur vers le pôle Nord ou vers le pôle Sud, et ignorent aussi dans quel sens orienter l'accélération qui résulte de ce produit aberrant. Pile ou face, c'est aussi sûr.
Réécriture en notations cohérentes (tensorielles, donc).Or ces mathématiques ci-dessus - de surcroît sur bases incohérentes - sont assez inutiles puisque dans quatre cas sur six le principe général de conservation du moment angulaire suffit à prédire les trajectoires inertielles réelles, par rapport au repère terrestre. Pour les deux cas non couverts par la conservation du moment angulaire, c'est la composition des vitesses angulaires qui donne la réaction d'inertie centrifuge corrigée. Il va suffire de prendre le référentiel terrestre, d'examiner deux situations, l'une à l'équateur, l'autre près du pôle Nord, et les trois directions de vitesses : vers le bas, vers le Sud, vers l'Est. Puis il ne restera plus qu'à résumer cela mathématiquement.
A l'équateurChute verticale, donc diminution du rayon, augmentation inversement proportionnelle de la vitesse angulaire totale pour maintenir le moment angulaire constant, si la chute est non contrainte ==> déviation vers l'Est.
Vitesse vers le Sud : effet nul.
Vitesse vers l'Est : augmentation de la vitesse angulaire totale ==> déviation vers le haut (par inertie centrifuge accrue).
A la limite, regarder les satellites géostationnaires.
Près du pôle NordChute verticale : effet nul.
Vitesse vers le Sud : augmentation du rayon, donc ralentissement de la rotation pour maintenir le moment angulaire constant, déviation vers l'Ouest.
Vitesse vers l'Est : augmentation de la vitesse angulaire totale ==> déviation vers le Sud (par inertie centrifuge accrue).
Calcul quantitatifIl semble que des lecteurs aient des difficultés avec ce coefficient 2, en provenance du développement du carré d'une somme, d'où la période de parcours de cercle inertiel de 11 h 58 mn à la limite des hautes latitudes et basses vitesses, soit la moitié de la période stellaire de la Terre, ce qui ne manque pas de surprendre.
Vitesse tangentielleCommençons par le cas facile, de la vitesse Est-Ouest, où les vitesses angulaires, de la Terre et du mobile par rapport à la Terre sont coplanaires, donc s'ajoutent algébriquement. On va les noter par une seule lettre chacune, [tex]\Omega[/tex] et [tex]\omega[/tex], et en module seulement.
Vers l'Ouest :
[tex]\Omega_{total}^2 = (\Omega - \omega)^2 = \Omega^2 - 2.\Omega.\omega + \omega^2.[/tex]
Vers l'Est :
[tex]\Omega_{total}^2 = (\Omega + \omega)^2 = \Omega^2 + 2.\Omega.\omega + \omega^2.[/tex]
Donc ne considérer que le premier terme du développement limité, en [tex]2.\Omega.\omega[/tex], n'est valide que jusqu'à [tex]\omega[/tex] valant 8 à 10 % de [tex]\Omega[/tex]. C'est donc très vite invalide pour un missile, un obus, une balle de mousquetterie, et d'autant plus que la latitude est élevée.
Vitesse radialeA la distance r de l'axe polaire, une vitesse radiale de dr/dt modifie le moment angulaire, ce qui non seulement modifie l'accélération centripète imposée par la liaison, mais aussi exige une intervention tangentielle par le système de guidage, pour augmenter (dr/dt > 0) ou diminuer (dr/dt < 0) le moment angulaire et l'énergie cinétique du mobile.
Notons A le quotient du moment angulaire initial par la masse du mobile : r². [tex]\Omega[/tex].
A' le moment angulaire massique final = [tex](r+dr)^2. \Omega[/tex],
A'-A = [tex]\Omega.(2.dr +dr^2)\ = \ 2.\Omega.dr[/tex].
Cette différence a été obtenue par le moment moyen de l'accélération de Coriolis, durant le temps dt : [tex]\gamma_C.r.dt[/tex]
D'où [tex]\gamma_C = 2.\Omega.\frac{\delta{r}}{\delta t}[/tex], avec le signe + vers l'Est pour dr/dt > 0.
Mise en forme mathématiqueAccélération de Coriolis imposée par les liaisons de guidage avec le repère non galiléen en rotation : [tex]2\breve{\Omega}.\frac{\delta\vec{r}}{\delta t}[/tex]
(où [tex]\breve{\Omega}[/tex] désigne la vitesse angulaire de la Terre par rapport aux étoiles fixes, et [tex]\vec{r}[/tex] désigne la position dans le repère terrestre, donc [tex]\frac{\delta\vec{r}}{\delta t}[/tex] désigne sa vitesse dans le repère terrestre)
et elle est mesurée avec un accéléromètre qui soit assez sensible pour les conditions expérimentales choisies.
Pourquoi le coefficient 2 ? Parce qu'on développe le carré d'une somme de vitesses angulaires, et que l'accélération centripète en mouvement circulaire (à trajectoire contrainte, donc) est proportionnelle au carré de la vitesse angulaire (totale).
[tex]\breve{\Omega}[/tex] est un tenseur antisymétrique de rang deux (ce qu'il vaut mieux désigner de façon plus brève en "tourneur" par opposition à "vecteur"). Il est contenu dans la direction de plan équatoriale, et son sens de rotation est le sens terrestre de rotation. Fin des conventions arbitraires et anti-physiques, fin de l'interdiction des changements de base non orthonormés qui faisaient tout sauter, l'outil tensoriel fait tout ce qu'il a à faire, et il le fait correctement, lui.
Alors qu'au contraire le mouvement inertiel libre (celui qui peut échapper à l'accélération de Coriolis) tourne
par rapport au repère terrestre comme la voûte du ciel par rapport à la Terre, et il se constate avec des bouées dérivantes dans la mer, ou des ballons-sondes dérivants, dans l'atmosphère.
Application aux courants de la MéditerranéeLien pour les documents :
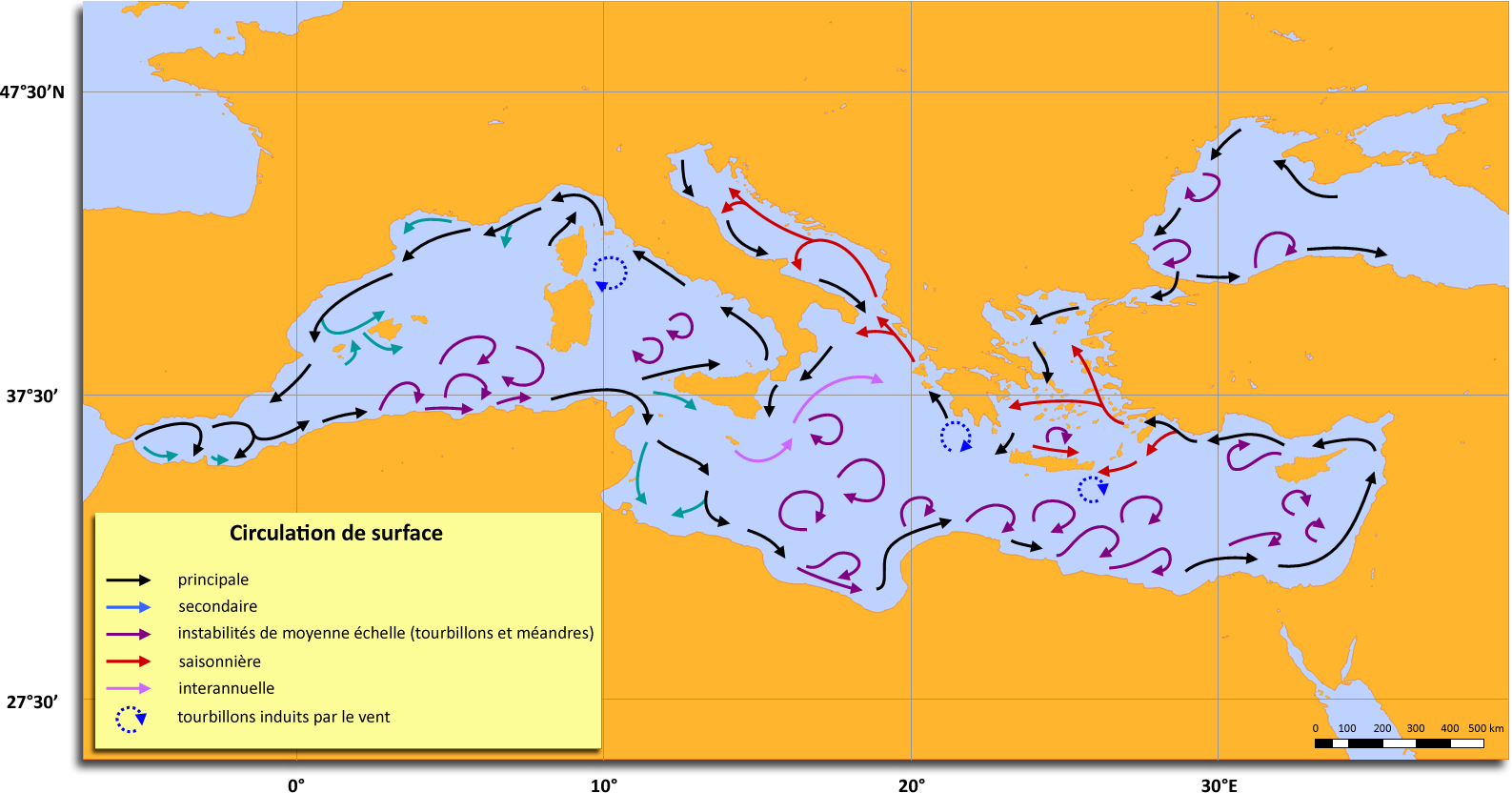
http://e-cours.univ-paris1.fr/modules/uved/envcal/html/oceans/2-exemples-phenomenes-physiques/tsm-courants-marins-surface/2-2-circulation-oceanique-mediterranee.htmlLa grande complexité se réduit à trois principes simples :
a. Le moteur est Gibraltar : entrée d'eaux Atlantiques de surface pour compenser l'évaporation méditerranéenne.
b. Le jet ENE (Est-Nord-Est) imposé par la côte de Ceuta, s'infléchit vers le Sud, en partie par inertie, dite "Coriolis" par le discours dominant, en partie aussi par rencontre avec le courant côtier SW qui revient par la côte de Murcie. Il bute alors sur la côte marocaine, et est contraint par la côte du Maghreb d'une part, puis par la côte Levantine, puis par la côte turque, d'autre part par les côtes siciliennes, puis italiennes, puis françaises et espagnoles à subir l'accélération de Coriolis, à longer les côtes.
c. Dans le détail interviennent les lois ordinaires de la circulation turbulente, avec contre-courants dans les criques et les golfes ; ce que connaissent tout kayakiste et tout canoéiste pratiquant l'eau vive, et que les marins connaissent aussi dans le golfe du Morbihan, et dans les rias et abers bretons.
 Total des membres: 62
Total des membres: 62 Dernier: MvMarcus70
Dernier: MvMarcus70 Total des messages: 5084
Total des messages: 5084 Total des sujets: 2368
Total des sujets: 2368 En ligne aujourd'hui: 11
En ligne aujourd'hui: 11 Record de connexion total: 138
Record de connexion total: 138 Membres: 0
Membres: 0 Invités: 9
Invités: 9 Total: 9
Total: 9


